Introduction

In the field of data science, we are often faced with the task of evaluating the performance of our models. One way to do this is by using metrics such as accuracy, precision, recall, F1-score, etc. However, when it comes to evaluating the performance of binary classifiers, two commonly used metrics are AUC-ROC and AUC-PR. These metrics measure the area under the receiver operating characteristic (ROC) curve and the precision-recall (PR) curve respectively. In this blog, we will explore the differences between these two metrics, including their definitions, calculations, interpretations, and use cases.

What are ROC and PR curves?

Before we dive into the metrics themselves, let’s take a quick look at what ROC and PR curves are.

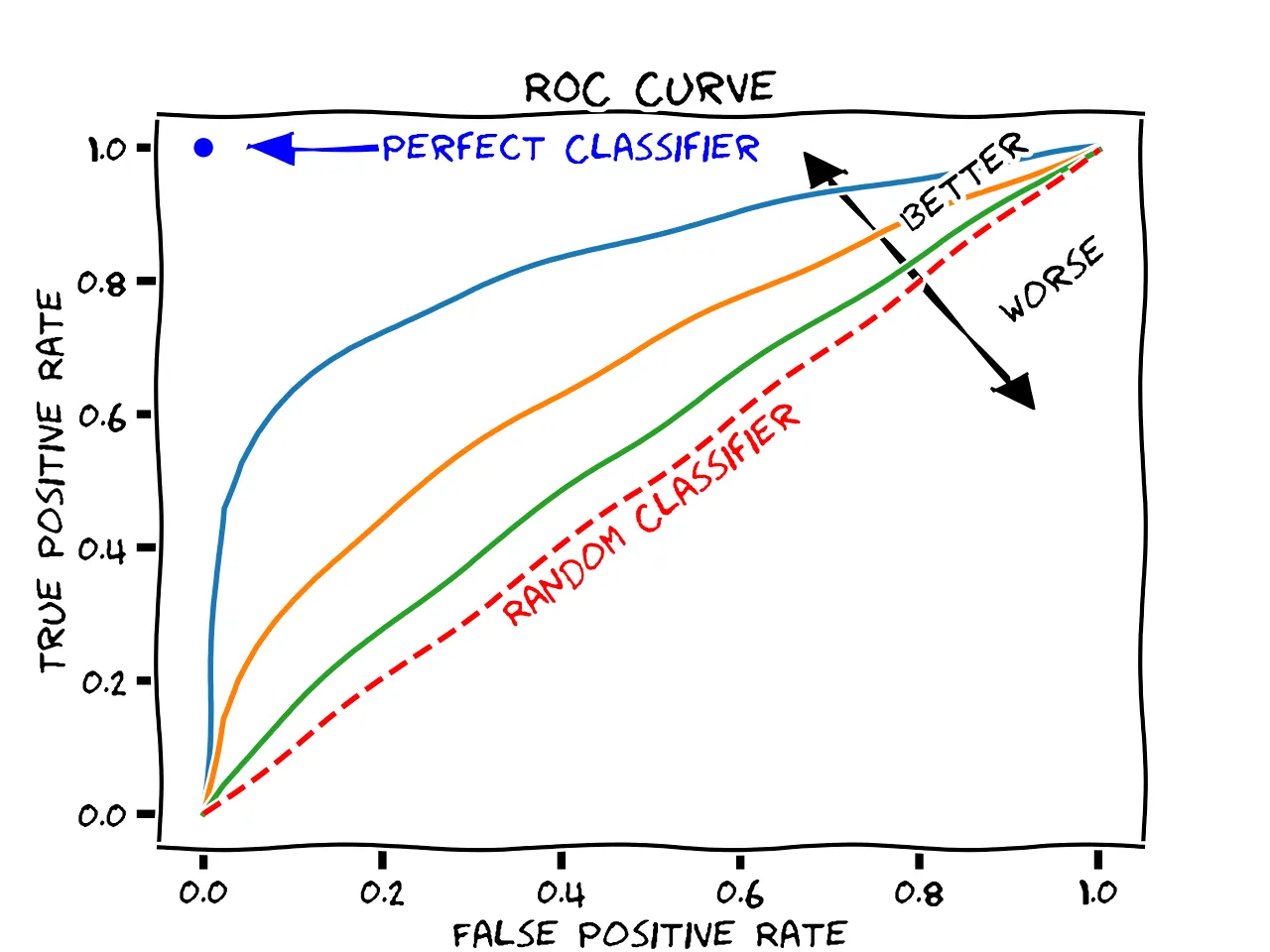
ROC curve: The ROC curve is a graphical representation of the trade-off between sensitivity (true positive rate) and specificity (false positive rate) for a binary classifier at different classification thresholds. The ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) for different values of the classification threshold. The area under the ROC curve (AUC-ROC) is a commonly used metric for evaluating the performance of binary classifiers.

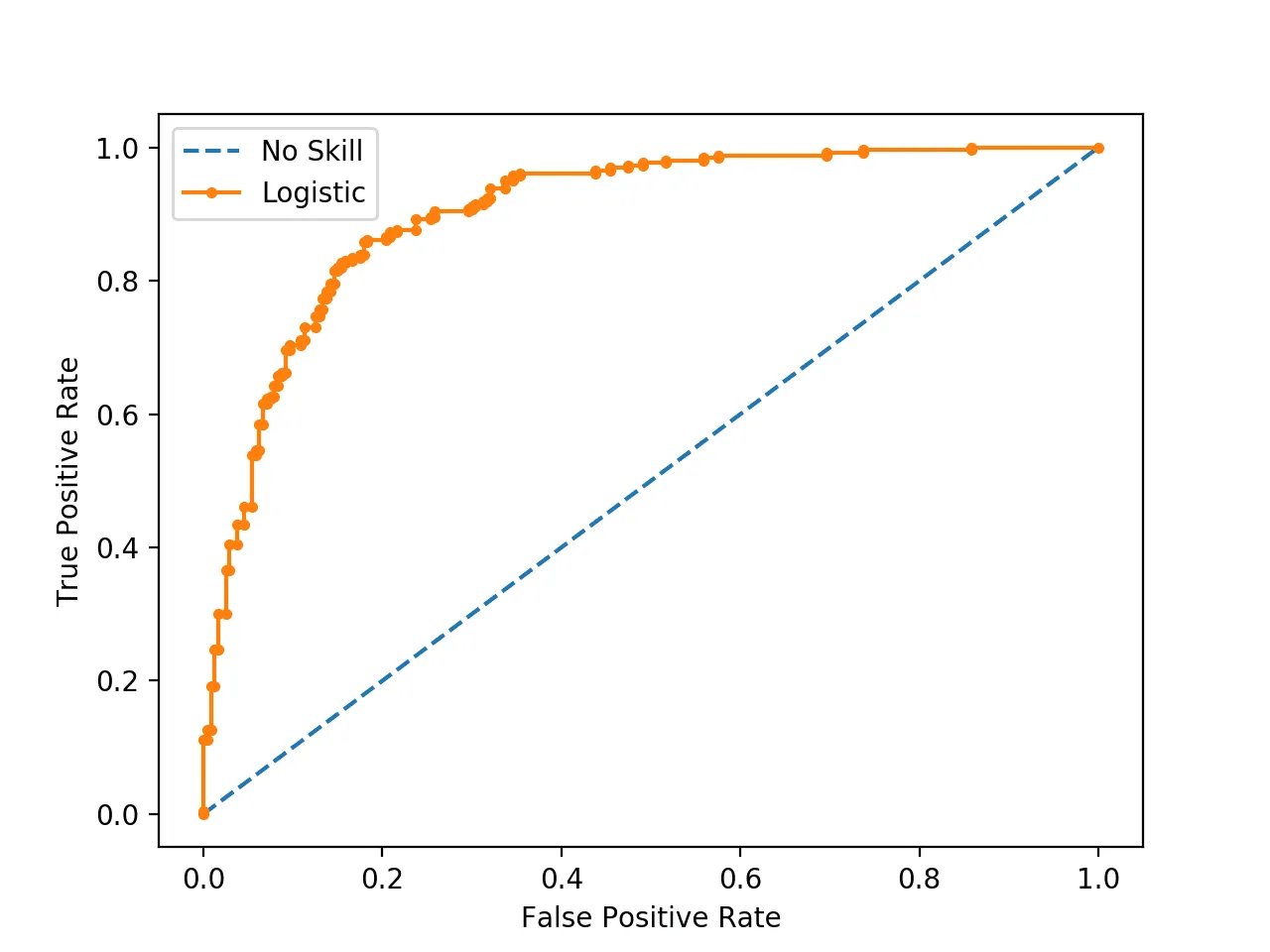
PR curve: The PR curve is a graphical representation of the trade-off between precision and recall for a binary classifier at different classification thresholds. The PR curve plots the precision against the recall for different values of the classification threshold. The area under the PR curve (AUC-PR) is another commonly used metric for evaluating the performance of binary classifiers.

Differences between AUC-ROC and AUC-PR

Now let’s explore the differences between AUC-ROC and AUC-PR.

Sensitivity vs. Precision

The ROC curve measures the trade-off between sensitivity and specificity, whereas the PR curve measures the trade-off between precision and recall. Sensitivity is the proportion of true positives that are correctly classified by the model, whereas precision is the proportion of true positives among all positive predictions made by the model. In other words, sensitivity measures how well the model can detect positive cases, whereas precision measures how well the model avoids false positives.

Imbalanced data

AUC-ROC is less sensitive to class imbalance than AUC-PR. In an imbalanced dataset, where one class is much more prevalent than the other, the ROC curve may look good even if the classifier is performing poorly on the minority class. This is because the ROC curve is mainly affected by the true negative rate (TNR), which is not affected by class imbalance. On the other hand, the PR curve is more affected by class imbalance, as it measures the performance of the classifier on the positive class only.

Interpretation

The AUC-ROC is generally interpreted as the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance. In other words, AUC-ROC measures the model’s ability to distinguish between positive and negative cases. On the other hand, AUC-PR is interpreted as the average precision of the classifier over all possible recall values. In other words, AUC-PR measures the model’s ability to predict positive cases correctly at all levels of recall.

Use cases

AUC-ROC is a good metric to use when the cost of false positives and false negatives is roughly equal, or when the distribution of positive and negative instances is roughly balanced. For example, in a medical diagnostic test where the cost of a false positive and a false negative is roughly the same, AUC-ROC is a suitable metric to use. On the other hand, AUC-PR is more suitable when the cost of false positives and false negatives is highly asymmetric, or when the positive class is rare. For example, in fraud detection or anomaly detection, where the cost of false positives is very high, AUC-PR is a more appropriate metric to use.

Calculation of AUC-ROC and AUC-PR

Now let’s look at how AUC-ROC and AUC-PR are calculated.

AUC-ROC: To calculate AUC-ROC, we first plot the ROC curve by calculating the TPR and FPR at different classification thresholds. Then, we calculate the area under the ROC curve using numerical integration or the trapezoidal rule. The AUC-ROC ranges from 0 to 1, with higher values indicating better classifier performance.

AUC-PR: To calculate AUC-PR, we first plot the PR curve by calculating the precision and recall at different classification thresholds. Then, we calculate the area under the PR curve using numerical integration or the trapezoidal rule. The AUC-PR ranges from 0 to 1, with higher values indicating better classifier performance.

Example using Python

Let’s see an example of how to calculate AUC-ROC and AUC-PR using Python. We will use the scikit-learn library for this purpose.

First, let’s import the necessary libraries and load the dataset:

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, average_precision_score

# Generate a random binary classification dataset
X, y = make_classification(n_samples=10000, n_features=10, n_classes=2, random_state=42)
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Next, let’s train a logistic regression model on the training set and make predictions on the test set:

# Train a logistic regression model on the training set
clf = LogisticRegression(random_state=42).fit(X_train, y_train)

# Make predictions on the test set
y_pred = clf.predict_proba(X_test)[:, 1]

Now, let’s calculate the AUC-ROC and AUC-PR scores:

# Calculate AUC-ROC score
roc_auc = roc_auc_score(y_test, y_pred)
print("AUC-ROC: ", roc_auc)

# Calculate AUC-PR score
pr_auc = average_precision_score(y_test, y_pred)
print("AUC-PR: ", pr_auc)

The output should be similar to the following:

AUC-ROC: 0.8823011439439692
AUC-PR: 0.8410720328711368

Conclusion

In conclusion, AUC-ROC and AUC-PR are two commonly used metrics for evaluating the performance of binary classifiers. While AUC-ROC measures the trade-off between sensitivity and specificity, AUC-PR measures the trade-off between precision and recall. AUC-ROC is less sensitive to class imbalance, whereas AUC-PR is more affected by it. AUC-ROC is suitable for situations where the cost of false positives and false negatives is roughly equal or when the distribution of positive and negative instances is roughly balanced. On the other hand, AUC-PR is more appropriate for situations where the cost of false positives and false negatives is highly asymmetric or when the positive class is rare. It is important to choose the appropriate metric based on the specific problem and the cost of misclassification.