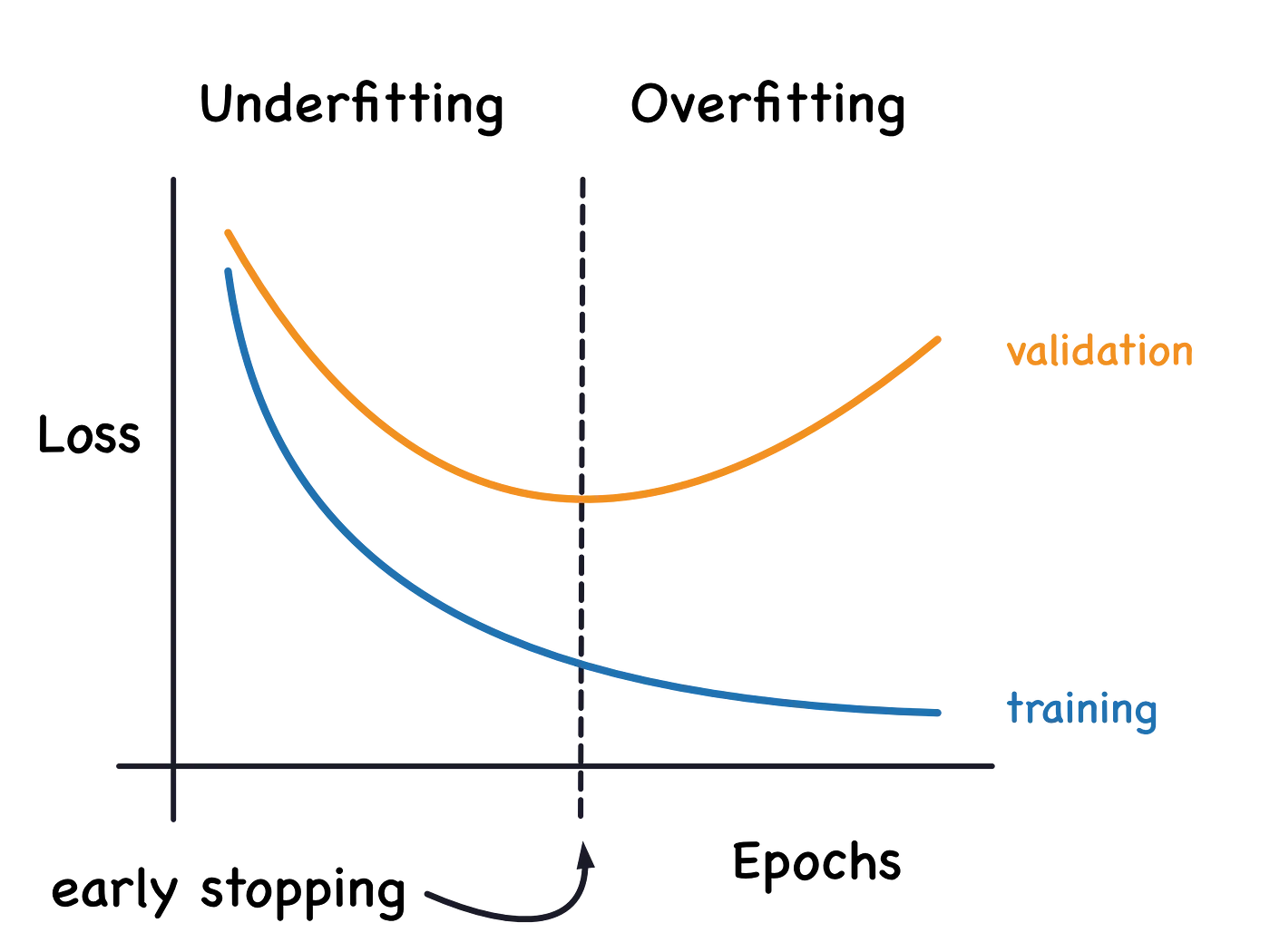
As the world becomes increasingly digitized, machine learning has emerged as a powerful tool to make sense of the vast amounts of data available to us. However, building accurate machine learning models is not always a straightforward task. One of the biggest challenges faced by data scientists and machine learning practitioners is ensuring that their models generalize well to new data. This is where the concepts of overfitting and underfitting come into play.
In this blog post, we’ll delve into the world of overfitting and underfitting in machine learning. We’ll explore what they are, why they occur, and how to diagnose and prevent them. Whether you’re a seasoned data scientist or just getting started with machine learning, understanding these concepts is crucial to building models that can make accurate predictions on new data. So let’s dive in and explore the world of overfitting and underfitting in machine learning.
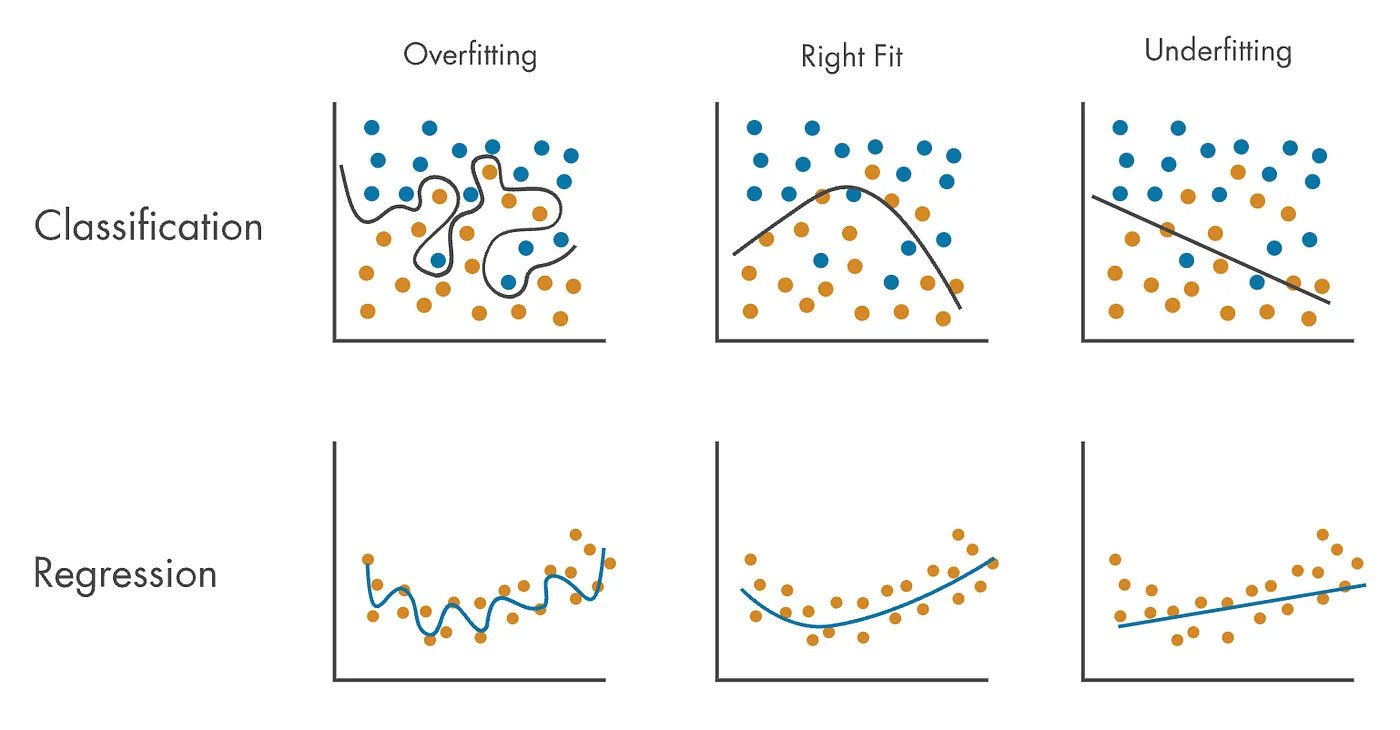
Overfitting
Overfitting occurs when the model fits the training data too closely, resulting in a model that is overly complex and not able to generalize well to new data. This happens when the model captures the noise in the training data instead of the underlying pattern. For example, consider a simple linear regression problem where we want to predict the height of a person based on their weight. If we have a dataset with 1000 training examples, we can easily fit a polynomial of degree 999 to perfectly fit the data. However, this model will not generalize well to new data because it has captured the noise in the training data instead of the underlying pattern.
One common way to detect overfitting is to split the data into a training set and a validation set. We then train the model on the training set and evaluate its performance on the validation set. If the model performs well on the training set but poorly on the validation set, it is likely overfitting. In other words, the model is too complex and memorises the training data instead of generalizing it to new data.
For example, suppose you train a model to classify images of dogs and cats. If the model is overfitting, it may achieve high accuracy on the training data (e.g., 98%), but its performance on new data may be significantly worse (e.g., 75%). This indicates that the model has memorized the training data, rather than learning the general patterns that would enable it to accurately classify new images.
Another way to detect overfitting is to look at the learning curve of the model. A learning curve is a plot of the model’s performance on the training set and the validation set as a function of the number of training examples. In an overfitting model, the performance on the training set will continue to improve as more data is added, while the performance on the validation set will plateau or even decrease.
There are several ways to prevent overfitting, including:
- Simplifying the model: One way to prevent overfitting is to simplify the model by reducing the number of features or parameters. This can be done by feature selection, feature extraction, or reducing the complexity of the model architecture. For example, in the linear regression problem discussed earlier, we can use a simple linear model instead of a polynomial of degree 999.
- Adding regularization: Another way to prevent overfitting is to add regularization to the model. Regularization is a technique that adds a penalty term to the loss function to prevent the model from becoming too complex. There are two common types of regularization: L1 regularization (also known as Lasso) and L2 regularization (also known as Ridge). L1 regularization adds a penalty term proportional to the absolute value of the parameters, while L2 regularization adds a penalty term proportional to the square of the parameters.
- Increasing the amount of training data: Another way to prevent overfitting is to increase the amount of training data. With more data, the model will be less likely to memorize the training data and more likely to generalize well to new data.
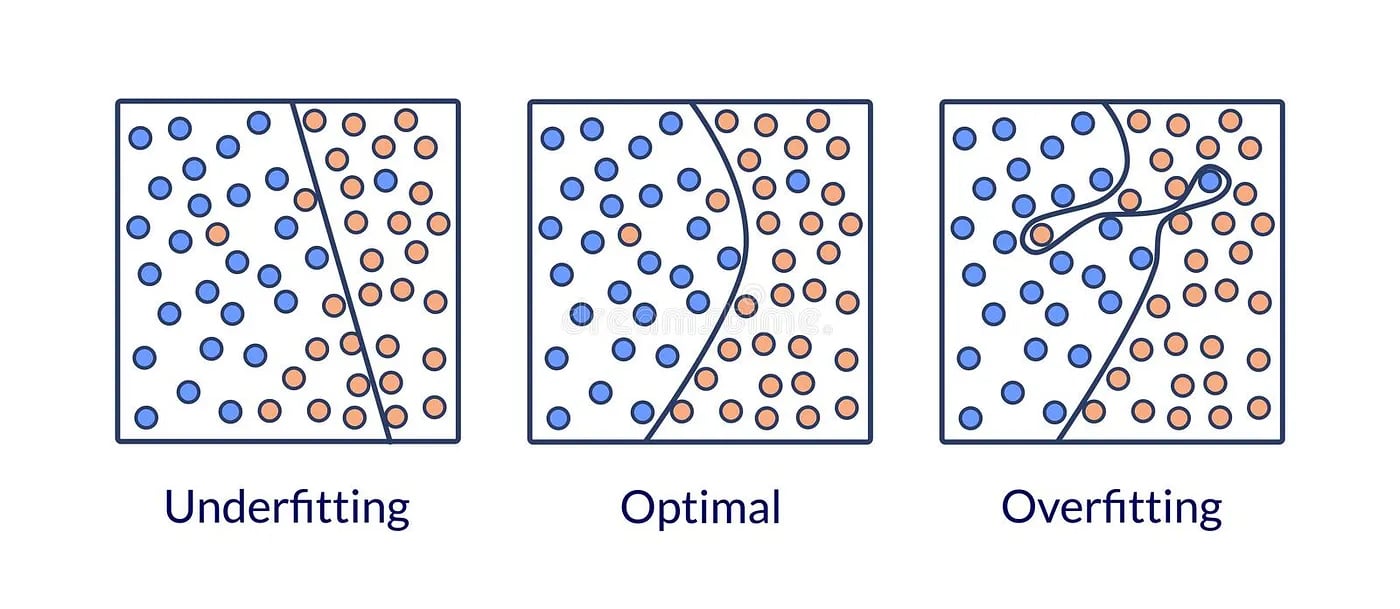
Underfitting
Underfitting occurs when the model is too simple to capture the underlying pattern in the data. In other words, the model is not complex enough to represent the true relationship between the input and output variables. Underfitting can occur when the model is too simple or when there are too few features relative to the number of training examples. For example, consider a simple linear regression problem where we want to predict the height of a person based on their weight. If we use a linear model to fit the data, we may not capture the curvature in the relationship between weight and height. In this case, the model is too simple to capture the true relationship between the input and output variables.
One common way to detect underfitting is to again look at the learning curve of the model. In an underfitting model, the performance of both the training set and validation set will be poor, and the gap between them will not decrease even as more data is added.
For example, if the model is underfitting, it may achieve a low R-squared value (e.g., 0.3) on the training data, indicating that the model explains only 30% of the variance in the target variable. The performance on the test data may also be poor, with a low R-squared value (e.g., 0.2) indicating that the model cannot accurately predict the prices of new, unseen data.
Similarly, the mean squared error (MSE) and root mean squared error (RMSE) of an underfitting model may be high on both the training and test data. This indicates poor generalization and training.
To prevent underfitting, we can:
- Increasing the model complexity: One way to prevent underfitting is to increase the model complexity. This can be done by adding more features or layers to the model architecture. For example, in the linear regression problem discussed earlier, we can add polynomial features to the input data to capture non-linear relationships.
- Reducing regularization: Another way to prevent underfitting is to reduce the amount of regularization in the model. Regularization adds a penalty term to the loss function to prevent the model from becoming too complex, but in the case of underfitting, we need to increase the model complexity instead.
- Adding more training data: Adding more training data can also help prevent underfitting. With more data, the model will be better able to capture the underlying pattern in the data.
Conclusion
In summary, overfitting and underfitting are two common problems in machine learning that can arise when training a predictive model. Overfitting occurs when the model is too complex and captures the noise in the training data instead of the underlying pattern, while underfitting occurs when the model is too simple to capture the underlying pattern in the data. Both these problems can be detected using a learning curve and can be prevented by adjusting the model complexity, regularization, or amount of training data. A well-generalizing model is one that is neither overfitting nor underfitting and can accurately predict new data.