Introduction

In the vast realm of data science, effectively managing high-dimensional datasets has become a pressing challenge. The abundance of features often leads to noise, redundancy, and increased computational complexity. To tackle these issues, dimensionality reduction techniques come to the rescue, enabling us to transform data into a lower-dimensional space while retaining critical information. Among these techniques, Linear Discriminant Analysis (LDA) shines as a remarkable tool for feature extraction and classification tasks. In this insightful blog post, we will delve into the world of LDA, exploring its unique advantages, limitations, and best practices. To illustrate its practicality, we will apply LDA to the fascinating context of the voluntary carbon market, accompanied by relevant code snippets and formulas.

Understanding Dimensionality Reduction

Dimensionality reduction techniques aim to capture the essence of a dataset by transforming a high-dimensional space into a lower-dimensional space while retaining the most important information. This process helps in simplifying complex datasets, reducing computation time, and improving the interpretability of models.

Dimensionality reduction can also be understood as reducing the number of variables or features in a dataset while preserving its essential characteristics. By reducing the dimensionality, we alleviate the challenges posed by the “curse of dimensionality,” where the performance of machine learning algorithms tends to deteriorate as the number of features increases.

What is the “Curse of Dimensionality”?

The “curse of dimensionality” refers to the challenges and issues that arise when working with high-dimensional data. As the number of features or dimensions in a dataset increases, several problems emerge, making it more difficult to analyze and extract meaningful information from the data. Here are some key aspects of the curse of dimensionality:

1. Increased Sparsity: In high-dimensional spaces, data becomes more sparse, meaning that the available data points are spread thinly across the feature space. Sparse data makes it harder to generalize and find reliable patterns, as the distance between data points tends to increase with the number of dimensions.
2. Increased Computational Complexity: As the number of dimensions grows, the computational requirements for processing and analyzing the data also increase significantly. Many algorithms become computationally expensive and time-consuming to execute in high-dimensional spaces.
3. Overfitting: High-dimensional data provides more freedom for complex models to fit the training data perfectly, which can lead to overfitting. Overfitting occurs when a model learns noise or irrelevant patterns in the data, resulting in poor generalization and performance on unseen data.
4. Data Sparsity and Sampling: As the dimensionality increases, the available data becomes sparser in relation to the size of the feature space. This sparsity can lead to challenges in obtaining representative samples, as the number of required samples grows exponentially with the number of dimensions.
5. Curse of Visualization: Visualizing data becomes increasingly difficult as the number of dimensions exceeds three. While we can easily visualize data in two or three dimensions, it becomes challenging or impossible to visualize higher-dimensional data, limiting our ability to gain intuitive insights.
6. Increased Model Complexity: High-dimensional data often requires more complex models to capture intricate relationships among features. These complex models can be prone to overfitting, and they may be challenging to interpret and explain.

To mitigate the curse of dimensionality, dimensionality reduction techniques like LDA, PCA (Principal Component Analysis), and t-SNE (t-Distributed Stochastic Neighbor Embedding) can be employed. These techniques help reduce the dimensionality of the data while preserving relevant information, allowing for more efficient and accurate analysis and modelling.

Types of Dimensionality Reduction

There are two main types of dimensionality reduction techniques: feature selection and feature extraction.

• Feature selection methods aim to identify a subset of the original features that are most relevant to the task at hand. These methods include techniques like filter methods (e.g., correlation-based feature selection) and wrapper methods (e.g., recursive feature elimination).
• On the other hand, feature extraction methods create new features that are a combination of the original ones. These methods seek to transform the data into a lower-dimensional space while preserving its essential characteristics.

Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) are two popular feature extraction techniques. PCA focuses on capturing the maximum variance in the data without considering class labels, making it suitable for unsupervised dimensionality reduction. LDA, on the other hand, emphasizes class separability and aims to find features that maximize the separation between classes, making it particularly effective for supervised dimensionality reduction in classification tasks.

Linear Discriminant Analysis (LDA)

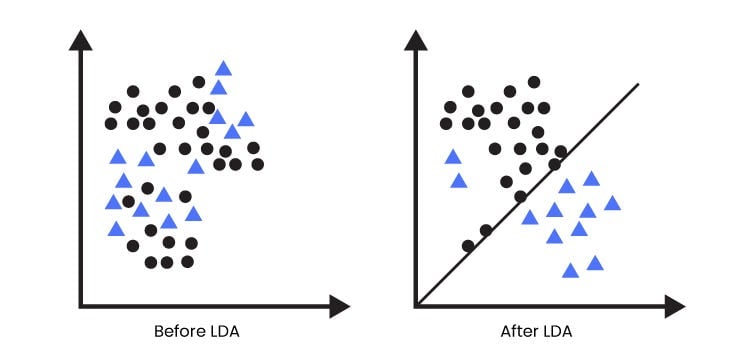
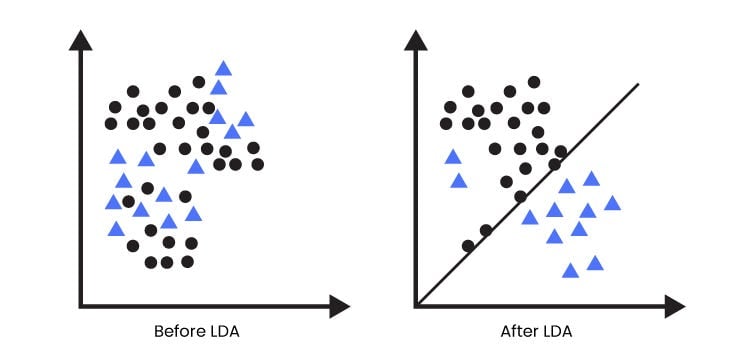
Linear Discriminant Analysis (LDA) stands as a powerful dimensionality reduction technique that combines aspects of feature extraction and classification. Its primary objective is to maximize the separation between different classes while minimizing the variance within each class. LDA assumes that the data follow a multivariate Gaussian distribution, and it strives to find a projection that maximizes class discriminability.

Steps for Implementing LDA

1. Import the necessary libraries: Start by importing the required libraries in Python. We will need scikit-learn for implementing LDA.
2. Load and preprocess the dataset: Load the dataset you wish to apply LDA to. Ensure that the dataset is preprocessed and formatted appropriately for further analysis.
3. Split the dataset into features and target variable: Separate the dataset into the feature matrix (X) and the corresponding target variable (y).
4. Standardize the features (optional): Standardizing the features can help ensure that they have a similar scale, which is particularly important for LDA.
5. Instantiate the LDA model: Create an instance of the LinearDiscriminantAnalysis class from scikit-learn’s discriminant_analysis module.
6. Fit the model to the training data: Use the fit() method of the LDA model to fit the training data. This step involves estimating the parameters of LDA based on the given dataset.
7. Transform the features into the LDA space: Apply the transform() method of the LDA model to project the original features onto the LDA space. This step will provide a lower-dimensional representation of the data while maximizing class separability.

Code Snippet: Implementing LDA in Python

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# Step 1: Import necessary libraries

# Step 2: Generate dummy Voluntary Carbon Market (VCM) data
np.random.seed(0)

# Generate features: project types, locations, and carbon credits
num_samples = 1000
num_features = 5

project_types = np.random.choice(['Solar', 'Wind', 'Reforestation'], size=num_samples)
locations = np.random.choice(['USA', 'Europe', 'Asia'], size=num_samples)
carbon_credits = np.random.uniform(low=100, high=10000, size=num_samples)

# Generate dummy features
X = np.random.normal(size=(num_samples, num_features))

# Step 3: Split the dataset into features and target variable
X_train = X
y_train = project_types

# Step 4: Standardize the features (optional)
# Standardization can be performed using preprocessing techniques like StandardScaler if required.

# Step 5: Instantiate the LDA model
lda = LinearDiscriminantAnalysis()

# Step 6: Fit the model to the training data
lda.fit(X_train, y_train)

# Step 7: Transform the features into the LDA space
X_lda = lda.transform(X_train)

# Print the transformed features and their shape
print("Transformed Features (LDA Space):\n", X_lda)
print("Shape of Transformed Features:", X_lda.shape)

In this code snippet, we have dummy VCM data with project types, locations, and carbon credits. The features are randomly generated using NumPy. Then, we split the data into training features (X_train) and the target variable (y_train), which represents the project types. We instantiate the LinearDiscriminantAnalysis class from sci-kit-learn and fit the LDA model to the training data. Finally, we apply the transform() method to project the training features into the LDA space, and we print the transformed features along with their shape.

Visualization of LDA

The scree plot is not applicable to Linear Discriminant Analysis (LDA). It is typically used in Principal Component Analysis (PCA) to determine the optimal number of principal components to retain based on the eigenvalues. However, LDA operates differently from PCA.

In LDA, the goal is to find a projection that maximizes class separability, rather than capturing the maximum variance in the data. LDA seeks to discriminate between different classes and extract features that maximize the separation between classes. Therefore, the concept of eigenvalues and scree plots, which are based on variance, is not directly applicable to LDA.

Instead of using a scree plot, it is more common to analyze the class separation and performance metrics, such as accuracy or F1 score, to evaluate the effectiveness of LDA. These metrics can help assess the quality of the lower-dimensional space generated by LDA in terms of its ability to enhance class separability and improve classification performance. The following Evaluation Metrics can be referred to for further details.

Advantages of LDA

LDA offers several advantages that make it a popular choice for dimensionality reduction in machine learning applications:

1. Enhanced Discriminability: LDA focuses on maximizing the separability between classes, making it particularly valuable for classification tasks where accurate class distinctions are vital.
2. Preservation of Class Information: By emphasizing class separability, LDA helps retain essential information about the underlying structure of the data, aiding in pattern recognition and improving understanding.
3. Reduction of Overfitting: LDA’s projection to a lower-dimensional space can mitigate overfitting issues, leading to improved generalization performance on unseen data.
4. Handling Multiclass Problems: LDA is well-equipped to handle datasets with multiple classes, making it versatile and applicable in various classification scenarios.

Disadvantages of LDA

While LDA offers significant advantages, it is crucial to be aware of its limitations:

1. Linearity Assumption: LDA assumes that the data follow a linear distribution. If the relationship between features is nonlinear, alternative dimensionality reduction techniques may be more suitable.
2. Sensitivity to Outliers: LDA is sensitive to outliers as it seeks to minimize within-class variance. Outliers can substantially impact the estimation of covariance matrices, potentially affecting the quality of the projection.
3. Class Balance Requirement: LDA tends to perform optimally when the number of samples in each class is approximately equal. Imbalanced class distributions may introduce bias in the results.

Practical Use Cases in the Voluntary Carbon Market

Linear Discriminant Analysis (LDA) finds practical use cases in the Voluntary Carbon Market (VCM), where it can help extract discriminative features and improve classification tasks related to carbon offset projects. Here are a few practical applications of LDA in the VCM:

1. Project Categorization: LDA can be employed to categorize carbon offset projects based on their features, such as project types, locations, and carbon credits generated. By applying LDA, it is possible to identify discriminative features that contribute significantly to the separation of different project categories. This information can assist in classifying and organizing projects within the VCM.
2. Carbon Credit Predictions: LDA can be utilized to predict the number of carbon credits generated by different types of projects. By training an LDA model on historical data, including project characteristics and corresponding carbon credits, it becomes possible to identify the most influential features in determining credit generation. The model can then be applied to new projects to estimate their potential carbon credits, aiding market participants in decision-making processes.
3. Market Analysis and Trend Identification: LDA can help identify trends and patterns within the VCM. By examining the features of carbon offset projects using LDA, it becomes possible to uncover underlying structures and discover associations between project characteristics and market dynamics. This information can be valuable for market analysis, such as identifying emerging project types or geographical trends.
4. Fraud Detection: LDA can contribute to fraud detection efforts within the VCM. By analyzing the features of projects that have been involved in fraudulent activities, LDA can identify characteristic patterns or anomalies that distinguish fraudulent projects from legitimate ones. This can assist regulatory bodies and market participants in implementing measures to prevent and mitigate fraudulent activities in the VCM.
5. Portfolio Optimization: LDA can aid in portfolio optimization by considering the risk and return associated with different types of carbon offset projects. By incorporating LDA-based classification results, investors and market participants can diversify their portfolios across various project categories, considering the discriminative features that impact project performance and market dynamics.

Conclusion

In conclusion, LDA proves to be a powerful dimensionality reduction technique with significant applications in the VCM. By focusing on maximizing class separability and extracting discriminative features, LDA enables us to gain valuable insights and enhance various aspects of VCM analysis and decision-making.

Through LDA, we can categorize carbon offset projects, predict carbon credit generation, and identify market trends. This information empowers market participants to make informed choices, optimize portfolios, and allocate resources effectively.

While LDA offers immense benefits, it is essential to consider its limitations, such as the linearity assumption and sensitivity to outliers. Nonetheless, with careful application and consideration of these factors, LDA can provide valuable support in understanding and leveraging the complex dynamics of your case.

While LDA is a popular technique, it is essential to consider other dimensionality reduction methods such as t-SNE and PCA, depending on the specific requirements of the problem at hand. Exploring and comparing these techniques allows data scientists to make informed decisions and optimize their analyses.

By integrating dimensionality reduction techniques like LDA into the data science workflow, we unlock the potential to handle complex datasets, improve model performance, and gain deeper insights into the underlying patterns and relationships. Embracing LDA as a valuable tool, combined with domain expertise, paves the way for data-driven decision-making and impactful applications in various domains.

So, gear up and harness the power of LDA to unleash the true potential of your data and propel your data science endeavours to new heights!